Trivial C# Random Exploitation
19 Aug 2025 - Posted by Dennis GoodlettExploiting random number generators requires math, right? Thanks to C#’s
Random, that is not necessarily the case! I ran into an HTTP 2.0 web service
issuing password reset tokens from a custom encoding of (new Random()).Next(min, max) output.
This led to a critical account takeover.
Exploitation did not require scripting, math or libraries. Just several clicks
in Burp. While I had source code, I will show a method of discovering and
exploiting this vulnerability in a black-box or bug-bounty style engagement.
The exploit uses no math, but I do like math. So, there is a bonus section on how to
optimize and invert Random.
The Vulnerability
I can’t share the client code, but it was something like this:
var num = new Random().Next(min, max);
var token = make_password_reset_token(num);
save_reset_token_to_db(user, token);
return issue_password_reset(user.email, token);
This represents a typical password reset. The token is created using Random(), and there is no
seed. This gets encoded to an alphanumeric token. The token is sent to the user
in email. The user can then log in with their email and token.
This may be trivially exploitable.
How the C# PRNG Works
Somehow documentation linked me to the following reference implementation. This
is not the real implementation, but it’s good enough. Don’t get into
the weeds here, the Random(int Seed) is only displayed for the sake of
context.
public Random()
: this(Environment.TickCount) {
}
public Random(int Seed) {
int ii;
int mj, mk;
//Initialize our Seed array.
//This algorithm comes from Numerical Recipes in C (2nd Ed.)
int subtraction = (Seed == Int32.MinValue) ? Int32.MaxValue : Math.Abs(Seed);
mj = MSEED - subtraction;
SeedArray[55]=mj; // [2]
mk=1;
for (int i=1; i<55; i++) { //Apparently the range [1..55] is special (Knuth) and so we're wasting the 0'th position.
ii = (21*i)%55;
SeedArray[ii]=mk;
mk = mj - mk;
if (mk<0) mk+=MBIG;
mj=SeedArray[ii];
}
for (int k=1; k<5; k++) {
for (int i=1; i<56; i++) {
SeedArray[i] -= SeedArray[1+(i+30)%55];
if (SeedArray[i]<0) SeedArray[i]+=MBIG;
}
}
inext=0;
inextp = 21;
Seed = 1;
}
This whole system hinges on the 32 bit Seed. This builds the internal state
(SeedArray[55]) with some ugly math. If Random is initialized without an
argument, the Environment.TickCount is used as Seed. All output of a PRNG
is determined by its seed. In this case, it’s the
TickCount
- essentially just time. So you can think of this whole algorithm as emailing you the time, just with a very odd encoding.
In some sense, you can even submit a time to encode. You do this, not with a URL parameter but by waiting. Wait for the right time and you get the encoding you want. What time, or event, should we wait for?
The Exploit
The documentation says it best.
In .NET Framework, the default seed value is derived from the system clock, which has finite resolution. As a result, different
Randomobjects that are created in close succession by a call to the parameterless constructor have identical default seed values and, therefore, produce identical sets of random numbers.
If we submit two requests in the same 1ms window, we get the same Seed, same
seed same output, same reset token sent to two email addresses. One email we own
of course, the other belongs to an admin.
How do we hit the 1ms window? We use the single packet attack.
Will it really work though?
Blackbox Methodology
You don’t want to go spamming admins with reset emails before you even verify the vulnerability. So make two accounts on the website that you control. While you can do the attack with one account, it’s prone to false positives. You’re sending two account resets in rapid succession. The second request may write a different reset token to the DB before the email service reads the first, resulting in a false positive.
Use Burp’s repeater groups to perform the single packet attack to reset both accounts. Check your email for duplicate tokens. If you fail, go on testing other stuff until the lockout window dies. Then just hit send again, likely you don’t need to worry about keeping a session token alive.
Note: Burp displays round trip time in the lower-right corner of Repeater.
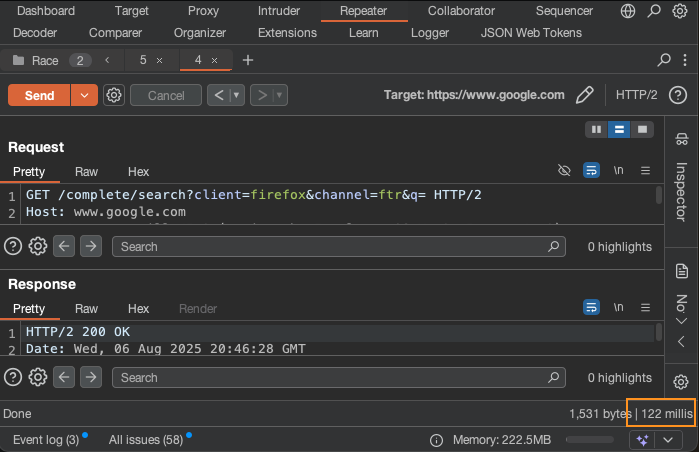
Keep an eye on that number. Each request has its own time. For me, it took about 10 requests before I got a duplicate token. That only occurred when the difference in round trip times was 1ms or less.
When launching the actual exploit, the only way to check if your token matches the victim account’s, is to log in. Login requests tend to be rate limited and guarded. So first verify with testing accounts. Use that to obtain a delta time window that works. Then, when launching the actual exploit, only attempt to log in when the delta time is within your testing bounds.
Ah… I guess subtracting two times counts as math. Exploiting PRNG’s always require math.
Wrapping Up
This attack is not completely novel. I have seen similar attacks used in CTFs. It’s a nice lesson on time though. We control time by waiting, or not waiting. If a secret token is just an encoded time, you can duplicate them by duplicating time.
If you look into the .NET runtime enough, you can convince yourself this attack
won’t work. Random has more then one implementation, the one my client should have used does not seed by
time.
I can even prove this with dotnetfiddle.
This is like the security version of “it works on my computer”. This is why we
test “secure” code and why we fuzz with random input. So try this exploit next
time you see a security token.
This applies to more then just C#’s Random. Consider Python’s uuid?
The documentation warns of potential
collisions due to lack of “synchronization” depending on “underlying platform”,
unless safeUUID is used. I wonder if the attack will work there? Only one way
to find out.
The fix for weak PRNG vulnerabilities is always to check the documentation. In this case you have to click the “Supplemental API remarks for Random.” in the “Remarks” section to get to the security info where it says:
To generate a cryptographically secure random number, such as one that’s suitable for creating a random password, use one of the static methods in the System.Security.Cryptography.RandomNumberGenerator class`.
So C# use RandomNumberGenerator instead of Random.
Bonus: Cracking C#’s Old Random Algorithm
Ahead is some math. It’s not too bad, but figured I would warn you. This is the
“hard” way to exploit this finding. I wrote a library that can predict the
output of Random::Next. It can also invert it, to go back to the seed. Or you
can find the first output from the seventh output. None of this requires brute
force, just a single modular equation. The code can be found here.
I intended this to be a fun weekend math project. Things got messed up when I found collisions due to an int underflow.
Seeding Is All Just Math
Let’s look at the seed algorithm, but try to generalize what you see. The
SeedArray[55] is obviously the internal state of the PRNG. This is built up
with “math”. If you look closely, almost every time SeedArray[i] is
assigned, it’s with a subtraction. Right afterward you always see a check, did
the subtraction results in a negative number? If so, add MBIG. In other words,
all the subtraction is done mod MBIG.
The MBIG value is Int32.MaxValue, aka 0x7fffffff, aka 2^31 - 1. This is a
Mersenne prime. Doing math, mod’ing
a prime results in what math people call a Galois field.
We only say that because Évariste
Galois was so cool. A
Galois field is just a nice way of saying “we can do all the normal algebra
tricks we learned since middle school, even though this isn’t normal math”.
So, lets say SeedArray[i] is some a*Seed + b mod MBIG. It gets changed in a
loop though by subtracting some other c*Seed + d mod MBIG. We don’t need that
loop - algebra says to just (a+c)*Seed + (b+d) Mod MBIG. By churning through
the loop doing algebra you can get every element of SeedArray in the form
of a*Seed + b mod MBIG
Every time the PRNG is sampled, Random::InternalSample is called. That is
just another subtraction. The result is both returned and used to set some
element of SeedArray. It’s just some equation again. It’s still in the Galois
field, it’s still just algebra and you can invert all of these equations. Given
one output of Random::Next we can invert the corresponding equation and get
the original Seed.
But, we can do more too!
csharp_rand.py library
The library I made builds SeedArray from these equations. It will output in
terms of these equations. Let’s get the equation that represents the first
output of Random for any Seed:
>>> from csharp_rand import csharp_rand
>>> cs = csharp_rand()
>>> first = cs.sample_equation(0)
>>> print(first)
rand = seed * 1121899819 + 1559595546 mod 2147483647
This represents the first output of Random for any seed. Use .resolve(42)
to get the output of new Random(42).Next().
>>> first.resolve(42)
1434747710
Or invert and resolve 1434747710 to find out what seed will produce
1434747710 for the first output of Random.
>>> first.invert().resolve(1434747710)
42
This agrees with (dotnetfiddle).
See the readme for more complicated examples.
An int Underflow in Random
Having just finished my library, I excitedly showed it to the first person who would listen to me. Of course it failed. There must be a bug and of course I blamed the original implementation. But since account takeover bugs don’t care about my feelings, I fixed the code… mostly…
In short, the original implementation has an int underflow which throws the
math equations off for certain seed values. Only certain SeedArray elements
are affected. For example, the following shows the first output of Random
does not need any adjustment, but 13th output does.
>>> print(cs.sample_equation(0))
rand = seed * 1121899819 + 1559595546 mod 2147483647
>>> print(cs.sample_equation(12))
rand = seed * 1476289907 + 1358625013 mod 2147483647 underflow adjustment: -2
So the 13th output will be seed * 1476289907 + 1358625013, unless the seed
causes an underflow, then it will be off by -2. The code attempts to decide
if the overflow occurs itself. This works great until you invert things.
Consider, what seed value will produce 908112456 as the 13th output of
Random::Next?
>>> cs.sample_equation(12).invert().resolve2(908112456)
(619861032, 161844078)
Both seeds, 619861032 and 161844078, will produce 908112456 on the 13th output
(poc). Seed 619861032 does it the proper
way, from the non-adjusted equation. Seed 619861032 gets there from the
underflow. This “collision” means there are exactly 2 seeds that produce the
same output. This means 908112456 is 2x more likely to occur on the 13th output
then the first. It also means there is no seed that will produce 908112458 on
the 13th output of Random. A quick brute force produced some 80K+ other
“collision” just like this one.
Bonus Conclusion
Sometimes the smart way is dumb. What started as a fun math thing ended up
feeling like death by a thousand cuts. It’s better to version match and
language match your exploit and get it going fast. If it takes a long time,
start optimizing while it’s still running. But before you optimize, TEST! Test
everything! Otherwise you will run a brute force for hours and get nothing.
Why? well maybe Random(Environment.TickCount) is not Random() because
explicitly seeding results in a different algorithm!
Ugh…. I am going to go audit some more
endpoints…

